3.9 KiB
透视投影
总体思路:
1.先透视变换 $P_{透视}$ 2.再投影 $P_{投影}$ 3.最终的变换矩阵 $T = P_{透视}P_{投影}$ 4.定点序列 $V_{new}=V_{origin}T $
1. 透视
1.1 一点透视
步骤:
(1) 进行平移变换,将三维形体平移到适当位 置l、m、n;
(2)进行透视变换;
(3)进行投影变换,向xoy平面作正投影变换,将结果变换到xoy平面上。
变换矩阵:
P_{透视}=\begin{bmatrix} 1&0&0&0\\0&1&0&0\\0&0&1&0\\L&M&N&1\end{bmatrix}
1.2 两点透视
步骤:
(1)先将三维形体平移到适当位置,使视点有一定 高度,且使形体的主要表面不会积聚成线;
(2)将形体绕y轴旋转一个φ⻆(φ<90 ̊),方向满足 右手定则;
(3)进行透视变换;
(4)最后向xoy面作正投影,即得二点透视图。
变换矩阵:
P_{透视}=\begin{bmatrix} 1&0&0&0\\0&1&0&0\\0&0&1&0\\L&M&N&1\end{bmatrix}\begin{bmatrix} cos(φ)&0&sin(φ)&0\\0&1&0&0\\-sin(φ)&0&cos(φ)&0\\0&0&0&1\end{bmatrix}
1.3 三点透视
步骤:
(1)首先将三维形体平移到适当位置;;
(2)将形体进行透视变换;
(3)然后使形体先绕y轴旋转φ⻆;
(4)再绕x轴旋转θ⻆;
(5)将变形且旋转后的形体向xoy面作正投影。
变换矩阵:
P_{透视}=\begin{bmatrix} 1&0&0&0\\0&1&0&0\\0&0&1&0\\L&M&N&1\end{bmatrix}\begin{bmatrix} cosφ&0&sinφ&0\\0&1&0&0\\-sinφ&0&cosφ&0\\0&0&0&1\end{bmatrix}\begin{bmatrix} 1&0&0&0\\0&cosθ&sinθ&0\\0&-sinθ&cosθ&0\\0&0&0&1\end{bmatrix}
2 投影
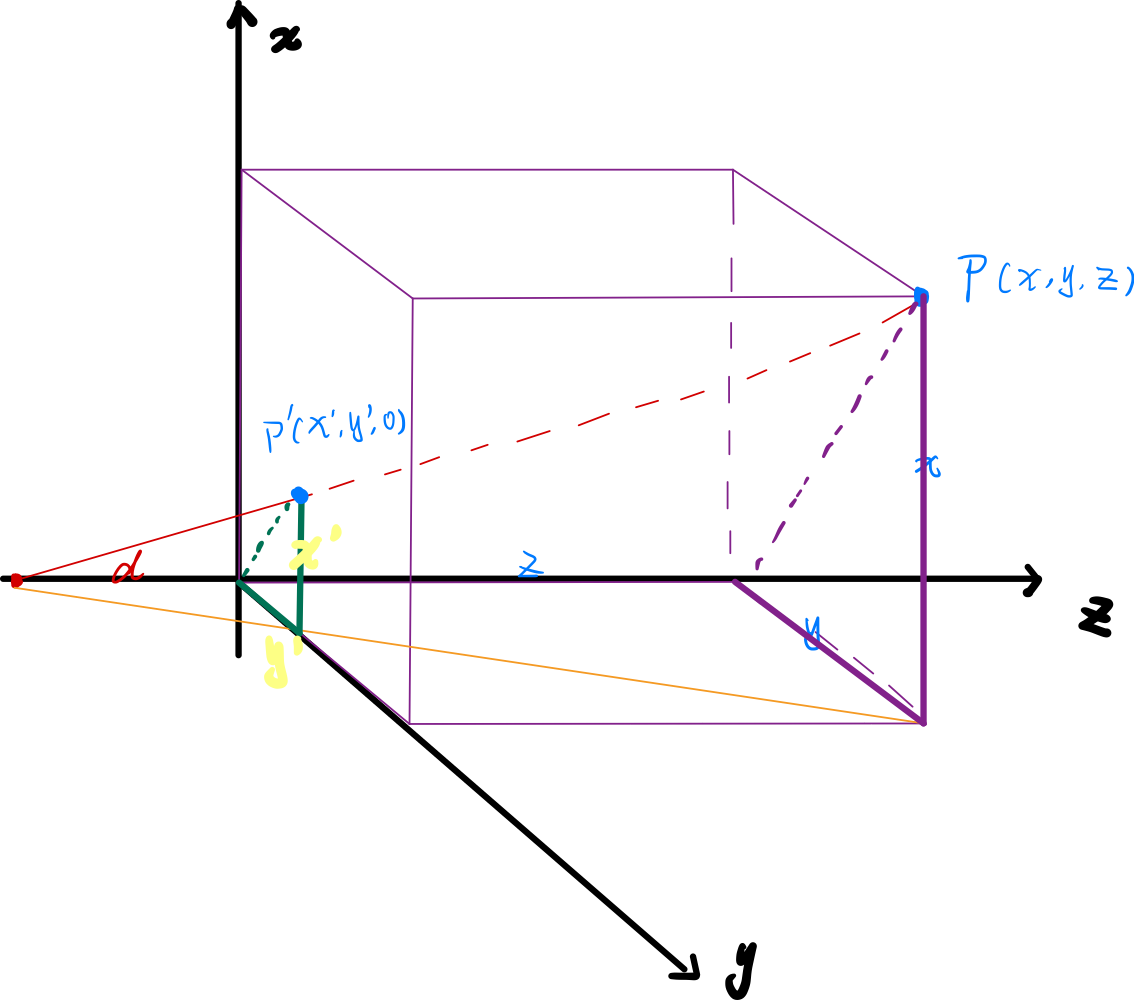
首先考虑这样一种最简单的情况,假设投影中心为坐标为 (0, 0, -d) ,空间中任意一点P(x,y,z),投影到$xOy$平面一点$P^’(x^’,y^’,0)$,由相似三角形易证:
x^’= \frac{d}{d+z}*x
y^’= \frac{d}{d+z}*y
易得,$P^’$的齐次坐标位为
[\frac{d}{d+z}*x,\frac{d}{d+z}*y,0,1]
即
[x,y,0,\frac{1+z}d]
P_{投影}=\begin{bmatrix} 1&0&0&0\\0&1&0&0\\0&0&0& \frac{1}{d} \\ 0&0&0&1 \\ \end{bmatrix}
P_{投影}=\begin{bmatrix} 1&0&0&0\\0&1&0&0\\0&0&1&0 \\ -x_0&-y_0&0&1 \\ \end{bmatrix}\begin{bmatrix} 1&0&0&0\\0&1&0&0\\0&0&0& \frac{1}{d} \\ 0&0&0&1 \\ \end{bmatrix} \begin{bmatrix} 1&0&0&0\\0&1&0&0\\0&0&1&0 \\ x_0&y_0&0&1\\ \end{bmatrix}= \begin{bmatrix} 1&0&0&0\\0&1&0&0\\\frac{x}{d}& \frac{y}{d}&0& \frac{1}{d} \\ 0&0&0&1\\ \end{bmatrix}
3 实例
假设初始顶点序列表示一个顶点在原点,边长为2的正方体,视点在(4,4,-2),投影平面在$xOy$。 用蓝色图形表示原图形;红色图形表示透视移动后的图形;黑色图形表示投影结果;绿色平面是投影平面;粉色虚线表示进行透视所进行的变换对应关系;黄色虚线表示投影进行的变换关系。
3.1 一点透视
假设移动距离L=6,M=5,N=1
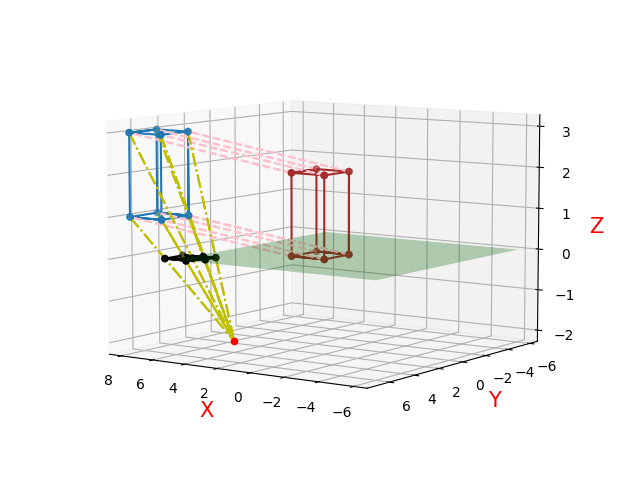
一点透视三维示意图
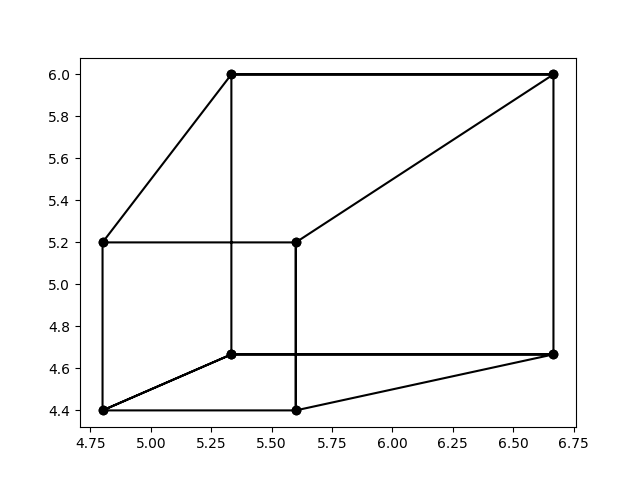
一点透视投影结果
3.2 二点透视
假设移动距离L=3,M=3,N=2,φ=60$^。$
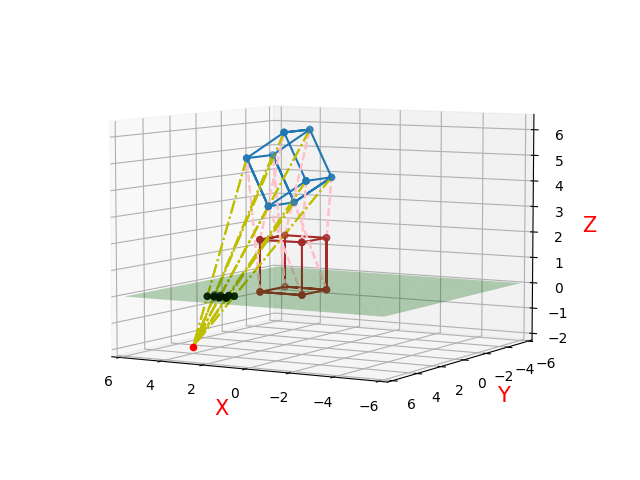
一二点透视三维示意图
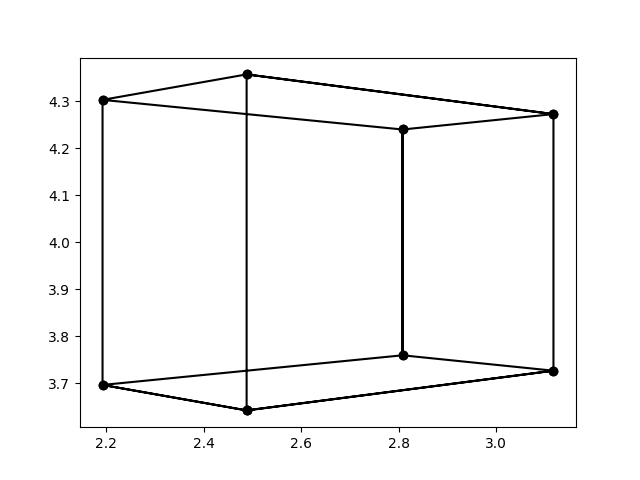
二点透视投影结果
3.3 三点透视
假设移动距离L=3,M=-3,N=2,φ=60$^。$,θ=60$^。$
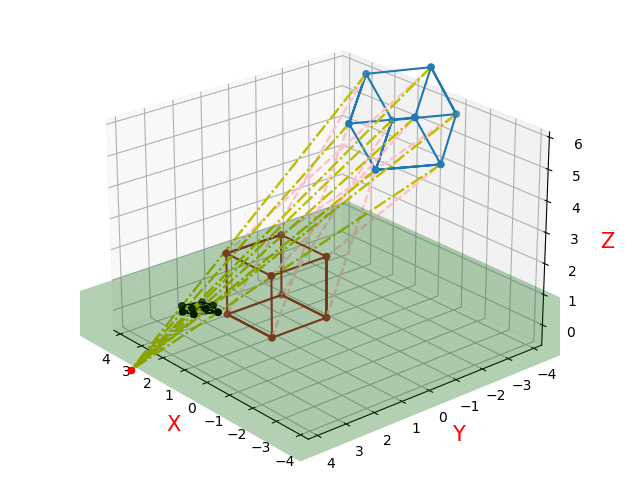
三点透视三维示意图
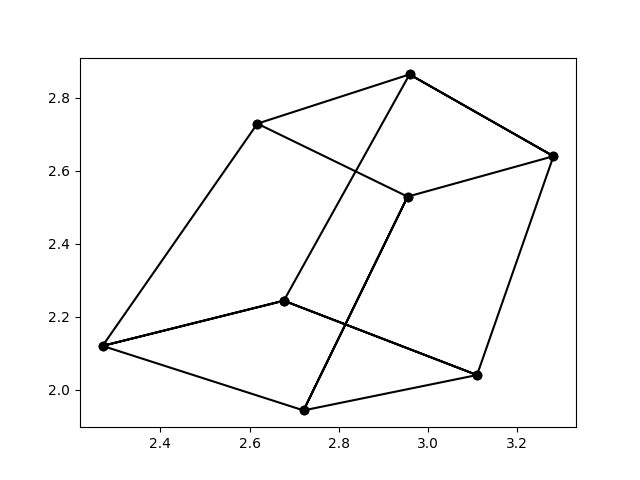
三点透视投影结果